How to calculate independent coordinates of traverse station with the help of distance and bearing ? | Comprehensive guide

The main steps that we follow for calculating the independent coordinates of each traverse station are:

1. Horizontal Angle Adjustment
2. Bearing computation of each side
3. Consecutive coordinate computation
4. Closing error calculation
5. Balancing the traverse
6. Independent coordinate calculation

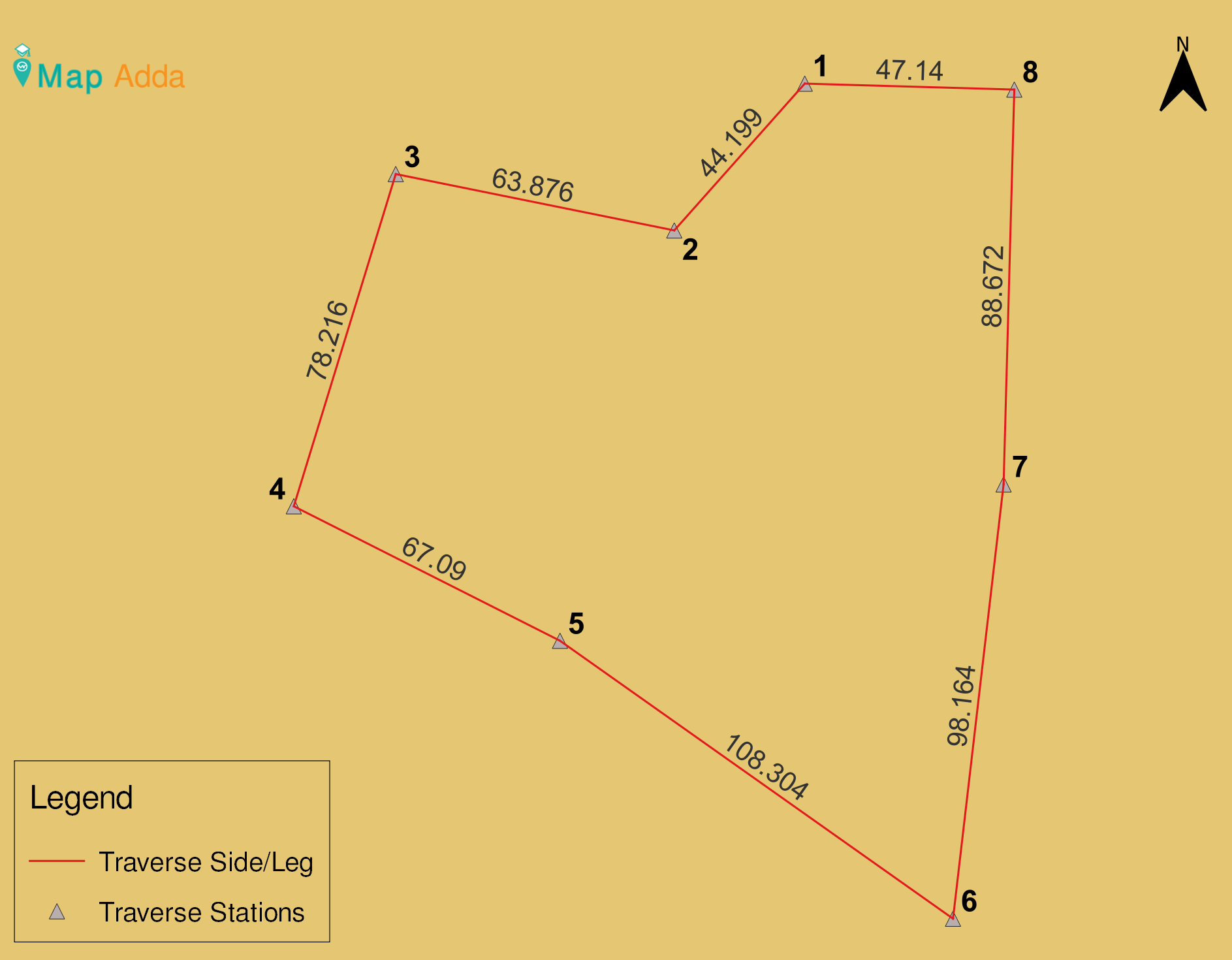
fig 1: showing traverse stations

fig 2: showing horizontal angle and distance measurement of all stations, Data credit: Bed Prasad Pangeni and team group A

Horizontal Angle Adjustment:

The sum of angles of a regular polygon is given by:

Sum= (2n±4)×90°

•  ‘+’ve if the traverse is done in clockwise direction (exterior angles)
• ‘-‘ve if the traverse is done in anticlockwise direction (interior angles)

 Where, n = total number of stations

Since, we have altogether 8 stations and the traverse is done in anticlockwise direction.

So, Theoretical Sum (ΣSum_T) = (2×8-4)×90°= 1080°

We have,

• Observed Sum (ΣSum_O) = 1080°0’40”
• Error in angular measurement can be calculated as:

Error (e) = ΣSum_T- ΣSum_O = 1080°- 1080°0’40”= – 0° 0’ 40”

Total error = – 0° 0’ 40” = -40”

Total correction =  -40”

Correction in each angle = -40”/8 = -5”

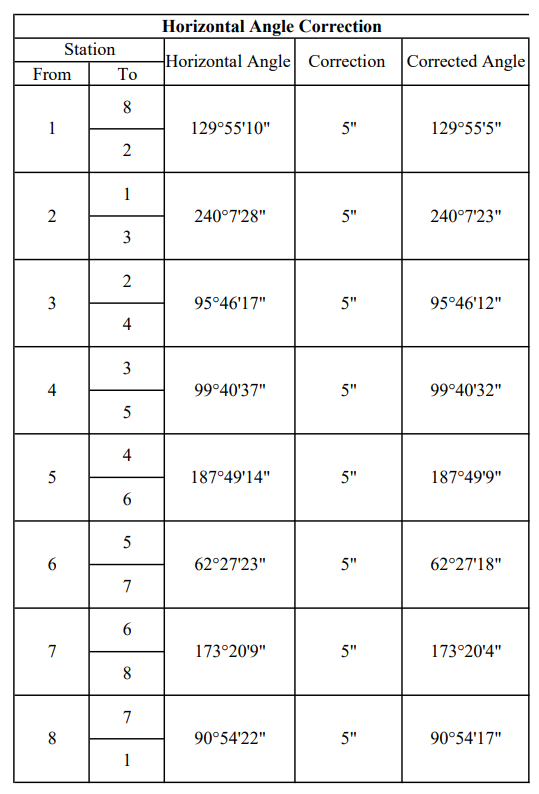
fig 3: showing horizontal angle correction

Bearing computation:

• Bearing of station 7-8 = 2^o  2’ 27’’ (which was measured on the field using mobile compass)
• From bearing of line 7-8 and corrected horizontal angle, the bearings of all other traverse legs can be computed by using formula:
• Bearing of next/forward line = Bearing of previous line + included angle between them

E.g Bearing of line joining ST8 – ST1 = Bearing of line joining (ST7-ST8) + angle at ST8

• If <180°, then add 180°
• If >180°, then subtract 180°
• If >540°, then subtract 540°

Accordingly, bearings are tabulated as

fig 4: showing bearing computation

Consecutive coordinate computation

The consecutive coordinates are expressed in term of latitude and departure which are used later to determine independent coordinates.

Latitude and departure are given by,

Latitude = L*sinθ and Departure = L*cosθ where

L = length of that line, θ= bearing of that respective line

The consecutive coordinates (latitude and departure) are tabulated as:

fig 5: showing consecutive coordinate calculation

Closing error

It is the distance by which the first point and last point of a close traverse do not meet at the same exact point.

In a closed loop traverse if the linear as well as angular measurement are correct, then the following condition must be satisfied:

Σ latitude = 0 and Σdeparture = 0

But due to  observational errors, the above condition is not satisfied and we have,

Σ latitude = 0.0176 and Σ departure = -0.2225

Balancing the traverse

It is the process of adjusting the consecutive co-ordinates of each line by applying correction to them in such a way that algebraic sum of latitudes and departures of a traverse equal to zero.

The following are some methods of balancing the traverse:

• Arbitrary method
• Bowditch’s method / Compass rule
• Transit method
• Graphical method
• Axis method

Here we are going to balance the traverse using bowditch method.

It is given by,

Correction in latitude of any line = (length of the line/ perimeter of traverse) ∗ Σlat

Correction in departure of any line = (length of that line/ perimeter of traverse) ∗ Σdept

The correction in latitude and departure are done by Bowditch’s rule as tabulated below:

fig 6: showing balancing the traverse

Independent coordinate calculation

After the traverse has been completely balanced (ie. Σlat.= 0 and Σdep. = 0) , the independent coordinates of all the traverse stations are calculated. If the coordinate of any one traverse station is known, then the independent coordinates of all other stations can be computed by using consecutive coordinates.

The independent coordinates of the first station (ie. ST1) was obtained previously through DGPS. It’s coordinates are:

Northing(N) = 3050431.6800

Easting(E) = 436948.1348

Elevation(Z) = 104.9146 m (Height above MSL)

The independent coordinates of other stations are computed and tabulated as:

Northing of next station = Northing of previous station + latitude of that line joining the stations

Easting of next station = Easting of previous station + departure of that line joining the stations

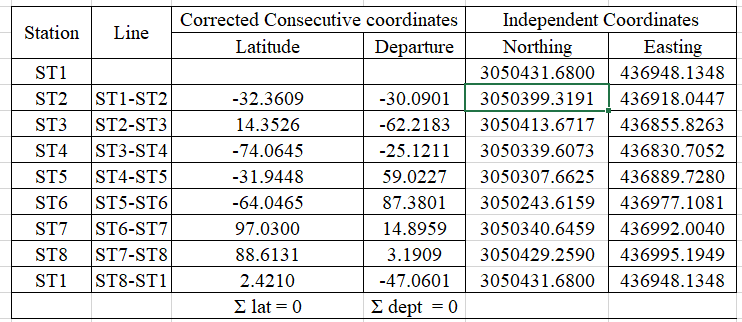
fig 7: showing independent coordinates

In this way, finally independent coordinates of a closed traverse can be calculated using included angles, bearing of a line and known a coordinate.

I hope it was helpful.